Drehinkrementalgeber

Funktionsweise

Fast alle Drehinkrementalgeber (auch Drehgeber, Drehimpulsgeber oder Encoder genannt) übermitteln Drehbewegungen mittels phasenverschobener Zustandsänderungen zweier Signale, A und B. Neben der Positionsänderung werden so auch Richtung und im weiteren Sinne sogar Geschwindigkeit nach Außen getragen. Das hört sich komplizierter an als es ist. Im Zeitdiagramm sieht das Ganze so aus: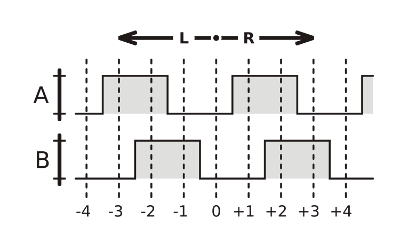

Wird der Drehknopf nach rechts, also im Uhrzeigersinn gedreht (R), durchläuft das Signalpaar AB nacheinander die Werte 00→10→11→01→00 ... usw. In anderer Richtung (L) ist die Abfolge entsprechend umgekehrt. Änderungen treten dabei immer nur an einem Signal auf, also A oder B. Zahlentheoretisch haben wir es mit einem zweibittigen Gray-Code hier zu tun.

Einmal formal ...

Das Verhalten eines Drehinkrementalgeber lässt sich formal in Form eines einfachen Mealy-Automaten beschreiben: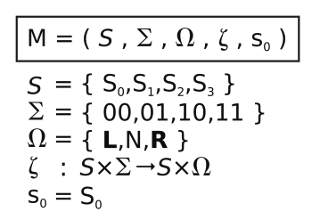

M besteht aus 5 Elementen:

S : Menge der Zustände, in unserem Fall 4
Σ : Menge der Eingaben, hier die 4 Kombinationen der AB-Pegel
Ω : Menge der Ausgaben. L für Linksbewegung, R für Rechtsbewegung und N für keine Bewegung
ζ : Zustandsübergangsfunktion
s₀: Anfangszustand.

Charakteristisch ist die Zustandsübergangsfunktion ζ (zeta). In ihr ist das Verhalten des ganzen Automaten hinterlegt. Sie bestimmt, welche Zustände mit welchen Eingaben welche Zustandswechsel vollziehen und welche Ausgaben dabei getätigt werden. Anschaulich läßt sich das an einem Zustandsdiagramm zeigen:

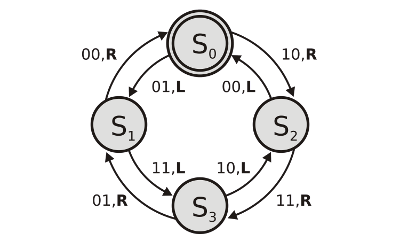
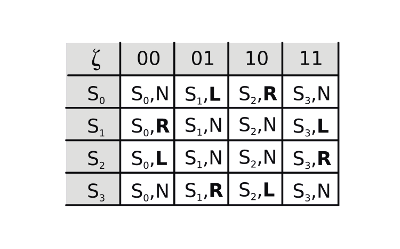
Los geht's im Zustand S₀. Eine Drehbewegung nach rechts bewirkt eine Zustandsänderung via S₂, S₃, S₁ usw. Bei entgegengesetzter Bewegung ist die Reihenfolge entsprechend umgekehrt. Zwecks besserer Nachvollziehbarkeit wurden im Diagramm die Übergänge zwischen S₀/S₃ bzw. S₁/S₂ weggelassen. Sie sind für die in der Theorie kontinuierlich ablaufenden Automaten unerheblich, können jedoch im realen Umfeld durchaus auftreten. Eine gute Darstellung der Funktion ζ ist die Wertetabelle:

In ihr finden sich auch die im Diagramm nicht eingezeichneten Übergänge. Die Definition ist vollständig, was bedeutet, dass zu jeder Kombination aus Zustand und Eingabe (S×Σ) eine eindeutige Ausgabe (S×Ω) existiert.

Einmal real ...

Die Abfrage des Drehinkrementalgeber gestaltet sich im Grunde ganz einfach. Hauptaufgabe dabei ist die Umsetzung der Zustandsübergangsfunktion ζ, bzw. ihrer o.g. Wertetabelle. Da sich hier die Folgezustände unmittelbar aus den Eingabewerten ableiten (ab → S_ab), halbiert sich die Größe des 2D-Feldes auf 16 Werte. Trotzdem sollte auf Systemen mit Harvard-Architektur die Wertetablle natürlich im Programmspeicherbereich abgelegt sein. Ausgaben L, N und R sind durch die Werte -1, 0 und +1 vertreten.
Wichtig ist, dass die Software möglichst jede Änderung des AB-Signals und damit jede Drehbewegung mitbekommt. Um diese Echtzeitanforderung erfüllen zu können, sollte der folgende Programmteil innerhalb eines Zeitinterrupts abgearbeitet werden. Wenn man das menschliche "Drehvermögen" als Grundlage nimmt, reichen IRQ-Aufrufe im Intervall von 1ms aus. Hier nun der Beispielcode in C:

static const SInt08 zeta[][4] = { { 0, -1, +1, 0 },
                                  { +1, 0, 0, -1 },
                                  { -1, 0, 0, +1 },
                                  { 0, +1, -1, 0 }
                                };
static const UInt08 encRaster = 2;    // Rasterstopps: 1,2 oder 4
static UInt08    encState = 0;    // Aktueller Zustand
static SInt08    encDelta = 0;    // Positionsveränderung
SInt08           encAB        // Eingabe aus A und B

encAB     = (!GetPin(ENC_A) << 1) + !GetPin(ENC_B);
encDelta += zeta[encState][encAB];
encState = encAB;
if( encDelta == encRaster || encDelta == -encRaster )
{ encDelta > 0 ? encPosition++ : encPosition--;
    encDelta = 0;
}

Die Signale A und B werden durch die Pins ENC_A und ENC_B eingelesen. Da die Pegel häufig "low-active" sind, werden beide vor der Zusammenstellung des Eingabewertes encAB invertiert.
Unterschiede gibt es bei den Haltepunkten. Manche Inkrementgeber vollziehen 4 Zustandswechsel, bevor sie in der Folgeposition einrasten, andere kommen mit der halben Phase aus. Theoretisch würde bereits ein einzelner Wechsel ausreichen um eine Positionsänderungen festzustellen, jedoch wären Fehler durch Prellen und "flatternde" Signale deutlich häufiger. Die Rastereinteilung ist in der Konstanten encRaster festgelegt. Erreicht die Anzahl Signalwechsel (der gleichen Richtung) den Wert in encRaster, hat das eine Veränderung des Wertes in encPosition um ±1 zur Folge.
Den Wert in encPosition kann man nun asynchron, z.B. im Bereich der Applikations-Hauptschleife, abfragen:

SInt08

GetRotEntPos(void)
{
    SInt08 value = 0;

    Atomic
    {   value = encPosition;
        encPosition = 0;
    }
    return value;
}

Dabei sollte sich der Aufrufer nicht zu viel Zeit lassen. encPosition hat mit seinen 8 Bits einen Wertebereich von -128 bis +127. Wird dieser aufgrund zu langsamer Abfrage über- bzw. unterschritten, ist der Wert des Drehgebers verloren. Grob gesagt: Mit einer 2er Rasterung ist man mit fünfmal pro Sekunde auf jeden Fall auf der sicheren Seite.

Jetzt gibt es eine gute und eine schlecht Nachricht. Die Schlechte ist: Es gibt Inkrementalgeber, die haben ihren Rasterpunkt genau an der Stelle liegen, wo auch ein Signalwechsel stattfindet. Das hat zur Folge, dass der Wechsel von einer Rasterposition zur Nächsten mal über 3, mal über 4 Signalwechsel geht. Je nach Bauart kann es also sein, dass AB z.B. 00→10→11→01→00 durchlaufen (4 Wechsel) oder eben dass AB kurz vor dem letzten Wechsel bei 01 verbleiben. Man kann sich also bei dieser Sorte Drehgebern nicht darauf verlassen, immer wieder in 00 einzurasten. Die gute Nachricht ist aber, dass man solches Verhalten ebenso mit dem oben gezeigten Automaten abbilden kann. Dazu ist lediglich eine Anpassung von ζ nötig. Genauer gesagt reicht es, die Wertetabelle ein wenig auszudünnen. Ist beispielsweise Signal B der "Wackelkandidat", sollten alle Zustandswechsel, die das Signal B betreffen, neutralisiert werden. Im Automaten bedeutet das, dass alle Wechsel zwischen S₀/S₁ und S₂/S₃ neutralisiert werden (N):

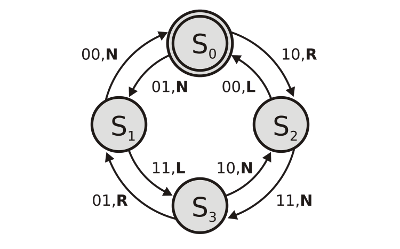
Damit halbiert sich zwar die Auflösung des Drehinkrementalgebers, aber das ist bei einer 4er-Rasterung völlig unerheblich. Machen wir's kurz: Der Austausch der Wertetabelle zeta gegen diese hier, löst das Problem:

static const SInt08 zeta[][4] = { { 0, 0, +1, 0 },
                                  { 0, 0, 0, -1 },
                                  { -1, 0, 0, 0 },
                                  { 0, +1, 0, 0 }
                                };

Weiterführende Informationen zum Thema Inkrementalgebern findet man jede Menge auf dem Netz.